Critical Thinking Math
Eye Level Critical Thinking Math takes students through a curriculum of study areas covering advanced mathematics concepts, skills and applications. Each level emphasizes critical thinking through reasoning skills, such as sequencing, comparing, planning, hypothesizing, analyzing, critiquing and developing of deep perception– that can all be applied in the student’s everyday life. Critical thinker students can develop, therefore, greater concentration, better study habits and increases self-confidence and self-esteem.

Critical thinking definition
Basic Thinking Math enables students to complete the foundation of mathematics and covers the following study areas: Numbers, Arithmetic, Measurement, and Equations.
The concept of critical thinking is derived from ancient Greek Kritikos meaning “discerning judgment based on standards”. Then it can actually be defined as “thinking explicitly aimed at well-founded judgment, utilizing appropriate evaluative standards such as logic in attempt to determine the true worth, merit or value of something”. When we think, we bring a variety of thoughts in some order. When the combined thoughts support each other and make sense together, the thinking is logical. Critical thinking tradition seeks ways of understanding the mind and training the intellect so that such “errors, blunders & distortions” of thought are minimized.

What is Critical Thinking?
Critical Thinking is The ability to think logically and make reasoned judgements.
Someone with Critical Thinking skills is able to do the following :
- Understand the logical connections between ideas
- Identify, construct and evaluate arguments
- Solve problems systematically
- Detect inconsistencies and mistakes in Reasoning
Eye Level Critical Thinking Mathematics


The Eye Level Critical Thinking Concept in based on teaching of the following curriculum:
- Relationship Analysis: Classification, relation, similarities, differences, irrelevances
- Geometry and spatial Sense: Spatial placement of directions, distances & location of figures and objects. The geometry and spatial sense ability helps to improve students’ skills in conservation, visualization and estimation
- Problem solving strategy: Data Analysis, tree diagram, pattern recognition, alternative methods, drawing diagrams, reverse calculation, deduction, trial and error.
- Reasoning: Reasoning, which is a higher order thinking skill, is a necessary skill in higher education and in working environment as students are required to critically evaluate statements and to make logical judgments. They will be able to understand and integrate a procedural process to reach a solution. With a developed reasoning skill, students will be able to show inferencing power that goes beyond factual information, and they will not easily be influenced by vague and ambiguous language. When Eye Level instructors teach students, they ask questions to guide them and avoid spoon feeding, so that the students can come up with a solution with minimal assistance. Memorizing the solution to a problem will lead to mastery of the specific problem short term. Critical thinking is a skill that Eye Level would like to nurture in students. At Eye Level, a good (or strong) critical thinker is equipped with the tools to solve effectively unfamiliar problems on a long term basis.

Numerical Figures assist in developing the concepts of number and quantity..
Numerical Figures

Students experience practical applications in Critical Thinking Math by solving applied mathematical problems using Eye Level Math Learning Materials.
Blocks and Shapes

Blocks and Shapes assist in developing depth perception by matching and finding the location of various shapes.
Clear Paper

Clear Paper is used to trace and copy various shapes. This helps students to develop their mental skills in relation to depth perception and location.
Colored Blocks

Colored Blocks assist in the understanding of numbers as well as length. As students manipulate Colored Blocks, they develop their perception of depth and location.
Mirror

Mirror activities require students to draw shapes symmetrically. This forms the basis for line symmetry that will be introduced in future studies.
Wooden Blocks

The manipulation of Wooden Blocks enables students to learn depth perception, location, and spatial relationships. This is crucial in the development of critical and analytical thinking skills.
Thinking Bricks

Thinking Bricks consist of three cuboids that can be used to stack up the bricks. (5 pieces, 2 sets)
Thinking Pentos
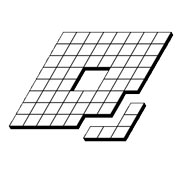
Thinking Pentos are used to build a model built by putting the sides of unit squares together. (12 pieces)
Thinking Cubes

Thinking Cubes are used to build a model that comprises the figures with concave surface built by putting together the faces of 3 or 4 cubes. (7 pieces)
Eye Level Critical Thinking Math Materials





